© Copyright JASSS


Giorgio Brajnik and Marji Lines (1998) 'Qualitative modeling and simulation of socio-economic phenomena'
Journal of Artificial Societies and Social Simulation vol. 1, no. 1, <https://www.jasss.org/1/1/2.html>
To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary
Received: 23-Oct-1997 Accepted: 13-Dec-1997 Published: 3-Jan-1998
 A version of this article in Portable Document Format (PDF) is also available. The PDF version is recommended if you want to print the article to a laser printer.
A version of this article in Portable Document Format (PDF) is also available. The PDF version is recommended if you want to print the article to a laser printer.

 Abstract
Abstract
- This paper describes an application of recently developed
qualitative reasoning techniques to complex, socio-economic
allocation problems. We explain why we believe traditional
optimization methods are inappropriate and how qualitative reasoning
could overcome some of these shortcomings. A case study is
presented where an authority is expected to devise a policy that
satisfies certain constraints. We describe how sets of rules of
thumb implementing such a policy can be analyzed and validated by
the decision maker using a program which automatically builds and
simulates qualitative models of the underlying dynamical system.
Such a program constructs and simulates models from incomplete
descriptions of initial states and functional relationships between
variables. We show that it nevertheless gives sufficient information
to the decision maker.
Keywords:- qualitative modeling, qualitative reasoning, decision making, allocation
 Introduction
Introduction
- 1.1
- National and international authorities must make difficult policy decisions regarding socio-economic problems which are complex, highly
interrelated, and subject to uncertainty and external disturbances.
Analytical and simulation models have proven useful in helping
decision makers to understand the processes involved in these complex
problem/policy contexts (for example, the Law of the Sea agreement
(Sebenius, 1984)). In this paper we describe a first attempt to apply
qualitative reasoning techniques to model the following problem: a
central authority must determine an allocation of national income
between consumption, capital investment, social services and
anti-pollution activity in order to ensure a sustainable time-path for
society.
- 1.2
- A typical model from environmental economics for our case could be
represented as an ordinary differential equation including two state
variables which influence welfare (utility): per capita
consumption (i.e., the proportion of the gross national product
"consumed" by a member of the society) and an index of
environmental quality (representing the amount of pollution present
in the natural environment).
In addition, state variables would be subject to constraints:
consumption cannot be greater than production, and other environmental
constraints may be related to the exhaustion of non-renewable energy
sources or to the pollution level endangering the life support
services of the environment, for example.
The solution of the problem, depending on its formulation, would
provide an authority with time-paths for (perhaps optimal) energy-use,
anti-pollution activity, emission taxes, incentive schemes for
investment in green technology.
- 1.3
- In this paper we propose the use of an alternative method, that of
qualitative modeling and simulation techniques recently developed
within the field of Artificial Intelligence to formulate and analyze
this kind of problems.
The benefits are that certain modeling activities can be automated and
the user can easily set up different "what-if" analysis scenarios.
Secondly, the simulation techniques are suited to the study of systems
that are only partially known. The simulators cope with this
incomplete knowledge by producing a concise qualitative description of
the all the possible outcomes, which may branch at points where
the information is ambiguous. This coverage guarantee is then
extremely useful in problems of designing a control policy since the
predicted outcomes would necessarily contain any unwanted
trajectories, that can therefore be detected, triggering a revision of
the control policy included in the model.
In addition, before applying numerical methods one has to resolve the
incompletely specified functional relationships among variables of the
system. This may lead to a costly activity of quantitative model
formulation and parameter identification. Qualitative simulation
techniques can be used as a preliminary step in analyzing
the consequences of certain qualitative relationships between
variables.
 Advantages Of Qualitative Reasoning
Advantages Of Qualitative Reasoning
- 2.1
- In the field of environmental economics much of the theoretical
modeling activity employs the optimal control framework based on
Pontryagin's maximum principle (e.g. Siebert, 1987). The goal is
to find values for the state variables that maximize (or minimize) an
objective function while at the same time satisfying a set of
constraints. The method of Lagrange multipliers can then be used to
set up a variational calculus problem.
- 2.2
- Economists tend to be interested in equilibrium (steady state)
solutions obtained by setting time derivates to zero and hence
transforming the differential system into a system of algebraic
equations. However, even equilibrium systems, in the presence of
nonlinear relations and/or more than two state variables, are
difficult to solve. Thus theorists frequently apply techniques of
comparative statics rather than solve for the trajectories of
interesting variables. For example, one might determine the direction
of change of the equilibrium environmental index if the discount rate
is higher or lower than hypothesized, rather than solve for the
optimal time-path of the environmental index.
- 2.3
- Let us suppose a steady state solution exists and can be determined.
The optimal solution will be sensitive to the hypothesized parameter
values and, of course, to the specific functional forms adopted in the
model.
However, the information set often provided on the hypothesized
implicit functional forms for production and welfare includes the
signs of the first and second partial (and perhaps cross-partial)
derivates. If explicit functional forms are volunteered they are
usually chosen for characteristics that compare favorably to real life
observations as well as mathematical simplicity. Most often power
functions are assumed whose coefficients are given a range rather than
an exact value.
- 2.4
- From this brief outline of the approach we can summarize four
objections to the use of the constrained control framework in policy
analysis of real world problems.
- Solvability.
- The rarity of worked-out solutions in
applications to economic policy problems suggests that it may not be a
practical technique for studying such problems (difficulty in solving
nonlinear systems with possibly more than two state variables).
- Complete knowledge.
- The precision of the solution method is
overwhelmed by necessary imprecision in the hypotheses (should a
solution be determined for a specific model, new solutions will have
to be determined when studying alternative assumptions that imply
changes in functional forms).
- Full certainty.
- Once a decision on the policy to be adopted,
it is assumed that the dynamics of the modeled system remain
certain and unchanged over the control horizon, typically infinity,
which is rather unrealistic.
- Optimization.
- The whole policy rests on optimization.
If that fails, there are no obvious guidelines for allocating resources.
- 2.5
- We believe that Qualitative Reasoning (QR) techniques
(Faltings and Struss, 1992, Kuipers, 1994) meet these objections.
- Solvability.
- The goal of the analysis is not a unique
analytical solution. We make use of simulation to follow all
possible state trajectories with the goal of formulating policies able
to keep these trajectories within certain limits.
- Complete knowledge.
- Qualitative models can be based on
extremely weak assumptions on the functional form relating two or
more variables in a differential equation and yet provide useful
results. In addition, numeric information in terms of ranges for
parameters and constants and envelopes for functional forms can be
added to the model, restricting the possible trajectories. Often,
the more knowledge available, the tighter the boundaries and the
fewer the qualitatively different trajectories.
- Full certainty.
- Simulation methods do cope with uncertainty in
states and models and propagate it across time up to any horizon of
interest, finite or infinite.
- Optimization.
- Allocation decisions can be informed by analysis
of the predicted trajectories of the system. These could serve as
guidelines in policy choice. Instead of focusing (only) on
optimization using a perhaps oversimplified model, decision makers
could focus on inadmissible trajectories and find corrective
actions to prevent them from occurring.
- 2.6
- A further advantage of studying non-optimal trajectories in this
context is that the entire spectrum of dynamic behavior is permitted
and analyzed, not just that described by equilibrium and transition to
equilibrium. This should be a better base from which to make policy
recommendations for the systems with complicated trade-offs which are
inherent to the analysis of economic growth and environmental quality.
 Qualitative Modeling And Reasoning
Qualitative Modeling And Reasoning
- 3.1
- Two research areas in the Qualitative Reasoning field are particularly
suited to deal with dynamic allocation problems, namely: automated
modeling and qualitative simulation.
- 3.2
- Automated modeling aims at developing programs which construct models
of the system under study and support the human modeler during model
management (i.e., a wide spectrum of activities encompassing problem
identification and formulation, model creation, implementation and
validation, solution of the problem and its interpretation).
Qualitative simulation (Kuipers, 1994) enables computers to
simulate dynamical systems and to yield useful predictions even in those
cases where only very rough and incomplete descriptions of systems
exists.
A recent research
branch called compositional modeling
(Falkenhainer and Forbus, 1991, Iwasaki and Low, 1991, Farquhar, 1994) aims at integrating
these two functionalities into programs that take as input a
(reusable) model of the domain and a description of a specific
situation, and produce predictive models and their predictions.
- 3.3
- Automated modeling and qualitative simulation are key ingredients for
tackling socio-economic problems that can be conceived in terms of a
set of interacting processes based on continuous variables.
- 3.4
- Compositional modeling offers the means to represent in a modular
(hence reusable) way fragments of equations that are automatically
composed into coherent models on the basis of a description of a
simulation scenario. In this way building different models for
analyzing different scenarios becomes a relatively easy task, that
builds on previous work. Additionally, the capability of these kind of
simulators to monitor the simulation and detect the situations in
which the boundary of the model validity region is hit, enables the
user to analyze scenarios where more than one model has to be used.
Compositional modeling programs cope automatically with such a model
switching.
- 3.5
- There are two main benefits deriving from the use of qualitative
simulators.
First is the ability to deal with non-parametric uncertainty, that is
uncertainty that is associated to functional relationships (where
analytical descriptions and numerical information about a function are
missing), instead of being simply included in
state/parameter descriptions.
Second is the abstraction that qualitative simulation is based
upon. The model that is used is a compact representation of a large
family of ordinary differential equations, and the simulation results
include the solutions of all the instances of the qualitative
model.
- 3.6
- In the following of this section we provide a brief description of
some of the tools and notions that are most relevant to our work.
We
start from the underlying qualitative simulator and then move to the
model building and simulation tool.
- 3.7
- We provide here a brief description of QSIM; for a deeper discussion
and for a thorough overview of applications of QSIM we
suggest reading (Kuipers, 1994).
- 3.8
- The input to QSIM is a qualitative differential equation (QDE)
which specifies:
- a set of variables (continuously differentiable
functions of time);
- a quantity space for each variable, specified in terms
of a totally ordered set of symbolic landmark values;
- a set of constraints expressing
algebraic, differential or monotonic relationships between
variables.
- 3.9
- A QDE is an abstract description of a set of ordinary differential
equations. The abstraction is achieved in two ways. Variables takes
values from the totally ordered set of symbolic landmarks. Each
landmark represents an unknown real number. For example, the starting
and equilibrium prices of a demand-supply market model can be
represented as two landmarks, whose real value is unknown, for the
variable price.
Secondly, monotonic relationships can be specified between variables,
like expressing that price levels are monotonically increasing with
respect to demand. Such a relation is an abstraction of an entire
family of (linear and nonlinear) functions. The only requirement is
that functions are smooth and that their derivatives have certain
signs.
- 3.10
- The output of QSIM is a set of behaviors. Each behavior is a
sequence of states, where a state is a mapping of variables to
qualitative values. A qualitative value represents the (qualitative)
magnitude of the variable (i.e., either a landmark or the open interval
between a pair of adjacent landmarks) and the direction of change of
the variable (i.e., the sign of its time derivative, represented as
dec, std, inc). Each state in a behavior describes either a time
point or an open temporal interval. Time is treated as another
qualitative variable, whose landmarks are automatically generated by
QSIM as critical points of other variables are identified.
- 3.11
- A monotonic function constraint represents an infinite set of real
valued functions. It has the general
form
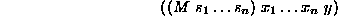
where each 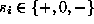 . Its meaning is given in terms of the subset of
continuous differentiable functions (
. Its meaning is given in terms of the subset of
continuous differentiable functions ( 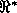 stands for the set of
real numbers extended with positive and negative infinity):
stands for the set of
real numbers extended with positive and negative infinity):
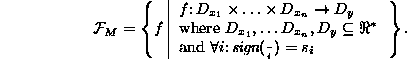
- 3.12
- For example, to specify that price level (P) depends simultaneously
on demand (D) and offer level (O), and it increases
with demand and it decreases with offer, the following constraint can be used:

- 3.13
- Simulation is based on a constraint satisfaction scheme: (i) successor
states are generated by propagating variables' values according to
continuity alone; (ii) successor states are filtered using constraints
and global criteria (e.g., unreachability of certain landmarks, finite
time for covering infinite distance) to decide which states are
admissible and which are inconsistent.
- 3.14
- QSIM produces zero or more qualitative behaviors that represent all
the possible trajectories from the initial state of all the instances
of the QDE (see figure 1).
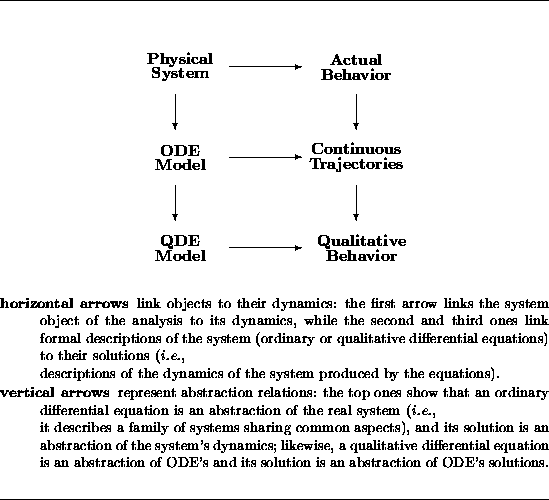
Figure 1: Qualitative simulation uses abstraction to cope with incomplete knowledge
- 3.15
- Hence QSIM is a sound tool. QSIM may yield too general
answers, though, being unable (because of the coarseness of the
qualitative representation) to remove from the output all the
behaviors that are mathematically impossible (spurious
behaviors). QSIM is said to be therefore incomplete. To
reduce the number of spurious behaviors several extensions have been
added to QSIM, each contributing to a significant reduction (yet not
a complete elimination) of spurious behaviors.
- 3.16
- One of these extensions enables semi-quantitative simulations
to be performed. That is, the basic qualitative representation is
augmented: each landmark may
be bounded with a numeric upper and lower bound, and each monotonic
function constraint may be bounded with a functional upper and lower
bound (envelope).
- 3.17
- The semantics of envelopes is easily understood in terms of set of
functions. As previously seen, any monotonic constraint is an abstract
description of a set of functions. An envelope for a constraint
restricts the set of functions that are associated to a constraint to
those that are bounded by the envelope.
- 3.18
- On the basis of numeric envelopes associated to monotonic constraints,
semi-quantitative simulators augment their predictions with numeric
bounds attached to each variable's value in each state. Such an
information is then used to rule out those behaviors that, although
being consistent with the qualitative differential equation, violate
some numeric bound.
Two techniques have been developed for implementing such extension to
qualitative simulation. The static envelopes technique developed
in (Berleant and Kuipers, 1988) propagates bounds (using algebraic constraints or
envelopes) throughout each time-point state and then uses the
mean-value theorem to constrain the values across time, for
time-interval states. The more
recent dynamic envelopes technique (Kay and Kuipers, 1993) constructs
extremal equations for the derivative of each state variable1. These extremal equations are then numerically integrated to
provide bounds on variable values across time intervals. Neither
technique strictly dominates the other. As a result, the bounds
provided by the two methods may be intersected, yielding sometimes
stronger predictions than either alone (Kay, 1996b, Kay, 1997).
- 3.19
- SQPC (Semi-Quantitative Physics Compiler)
(Farquhar and Brajnik, 1994, Brajnik, 1995) is an implemented approach to modeling and
simulation that performs self-monitoring simulations of
incompletely known, dynamic, piecewise continuous systems. SQPC
automatically constructs a model, simulates it, and monitors the
simulation in order to detect violations of model assumptions; when
this happens it modifies the model and resumes the simulation. SQPC
is built on top of the QSIM qualitative simulator.
- 3.20
- The input to SQPC is a domain model and scenario
specified in the SQPC modeling language. A domain model consists
of:
- A taxonomy of entity types: a hierarchy of types of
objects and associated relationships, called structural
relations. Types denote sets of objects, and the (built-in)
IS-A relation represents set inclusion. For example,
IS-A(funded-activities, activities) states that funded
activities are a particular case of activities. The user can define
domain-dependent relationships, such as supports(societies,
funded-activities) meaning that in a society certain funded
activities may take place.
- A set of quantity types: each quantity type is an
attribute of tuples of entity types which maps their instances onto
real-valued functions. More specifically, a quantity type QT
maps a tuple of entity types (
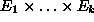 ) to a
set of functions, mapping time (
) to a
set of functions, mapping time (  ) into real
numbers.
A quantity
Q, instantiation of some QT on
) into real
numbers.
A quantity
Q, instantiation of some QT on 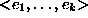 is a specific function of time:
is a specific function of time:
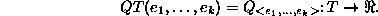
For example, one can define the quantity type
capital(productions)). If car-manufacturing is an instance
of productions, then capital(car-manufacturing) is a
specific function, mapping time to an amount of money. If Q is
a quantity then the term derivative(Q) denotes the quantity
representing the time derivative of Q.
- a set of quantified definitions, called model fragments,
each of which describes some aspect of the domain, such as physical
laws (e.g., natural abatement of pollution), processes (e.g., industrial
production), mechanisms (e.g., investment rules), and entities (e.g.,
population, environments). The idea is to represent separate
"pieces" of models and equations that can be automatically combined
into many different complete models, as opposed to provide already "packaged"
models. Each model fragment applies whenever there exists a set of
participants for whom the stated conditions are satisfied. The
specific system or situation being modeled is partially described by
the scenario definition, which lists a set of objects that are of
interest, some of their initial conditions, relations that hold
throughout the scenario, and boundary conditions.
Influences are compositional relations between variables that are
particularly convenient for asserting fragments of information that
can be composed into constraints. Three kinds of influences are
supported by SQPC.
An instantaneous influence such as 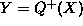 means that in the
absence of countervailing influences, an increase in X
causes an increase in
Y. Furthermore, once we determine the set of influences
affecting Y,
Y is functionally determined by the influencing variables.
means that in the
absence of countervailing influences, an increase in X
causes an increase in
Y. Furthermore, once we determine the set of influences
affecting Y,
Y is functionally determined by the influencing variables.
Algebraic influences provide additional information on the form
of the function f. SQPC's language offers four kinds of algebraic
indirect influences, one for each basic arithmetic operation.
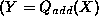 means that there exists a family of quantities
means that there exists a family of quantities
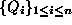 , with
, with 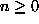 such that
such that 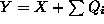 . Similarly for
. Similarly for 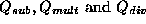 .
.
Finally, a dynamic influence such as 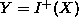 ) expresses
the fact that if there are no other countervailing influences, a
positive value of X causes an increase of Y. Direct
influences are equivalent to algebraic influences on the derivative of the
influenced variable (i.e.,
) expresses
the fact that if there are no other countervailing influences, a
positive value of X causes an increase of Y. Direct
influences are equivalent to algebraic influences on the derivative of the
influenced variable (i.e.,
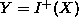

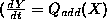 ).
).
A model fragment may assert other kinds of information besides
influences: inequalities between quantities and numerical magnitudes,
QSIM constraints or structural relationships.
- 3.21
- SQPC smoothly integrates symbolic with
numeric information, and is able to provide useful results even when
only part of the knowledge is numerically bounded. The domain model
includes symbolic or numeric magnitudes (both representing
specific real numbers, known with uncertainty; numeric magnitudes
constrain such numbers to lie within given ranges), dimensional
information (what does the quantity represent: money, money/time, amounts,
people, etc.), envelope schemas (stating the conditions under
which a specific monotonic function over a tuple of variables is
bounded by a pair of numeric functions) and tabular functions
(numeric functions defined automatically by interpolating
multi-dimensional data tables). The specific system or situation
being modeled is described by the scenario definition, which lists
objects that are of interest, some of the initial conditions,
relations that hold throughout the scenario, and possibly
time-varying boundary conditions on exogenous variables.
- 3.22
- SQPC employs a hybrid architecture in which the model building portion
is separated from the simulator. The domain model and scenario
induce a set of logical axioms. SQPC uses these logical
axioms to infer the set of model fragment instances that apply during
the time covered by the axioms (called the active model
fragments). Inferences performed by SQPC include those concerning
structural relationships between objects declared in the scenario, and
those aiming at computing the transitive closure of order
relationships between quantities. A complete set of
model fragment instances defines an initial value problem which is
given to the simulator in terms of equations and initial conditions.
If any of the predicted behaviors cross the boundaries of the current model the
process is repeated: a new set of axioms is constructed to describe the
system as it crosses the boundaries of the current model, another
complete set of active model fragments is determined, and another
simulation takes place.
- 3.23
- Recently, SQPC has been extended with the capability of simulating
non-autonomous systems, where the environment may affect the
simulated system through time-varying exogenous variables
(Brajnik, 1995).
Furthermore, using an appropriate language based on temporal logic,
the user can specify in the scenario description other kinds of
behavioral constraints, to focus the simulation
(Brajnik and Clancy, 1996a, Brajnik and Clancy, 1996b, Brajnik and Clancy, 1998).
- 3.24
- SQPC is proven to construct all possible sequences of initial value
problems that are entailed by the domain model and scenario; thanks to
QSIM correctness, it produces also all possible trajectories.
 The Authority's Problem
The Authority's Problem
- 4.1
- Let's return now to the problem mentioned in the introduction and use
it as a case study.
- 4.2
- Consider a central authority which has been charged with maintaining
the quality of life for the N members of its society within certain
limits. Quality of life for this problem is a function of two variables,
per capita consumption -- measured in gross domestic product (GDP/N) --
and an index of environmental quality -- measured by pollution in
parts per million (PPM) volume of atmospheric carbon dioxide, CO
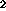 being the largest contributor to green house gases. The authority may
use any allocation scheme for assigning unconsumed national income
(capital resources) to those types of investments pertinent to the
task: increase capacity for producing consumer goods, given current
technology; spend on R&D to reduce unit emissions in the production
technology; increase capacity for abatement activity (in particular,
land use policies); augment family planning services and education
aimed at reducing the proportional growth rate of the population.
being the largest contributor to green house gases. The authority may
use any allocation scheme for assigning unconsumed national income
(capital resources) to those types of investments pertinent to the
task: increase capacity for producing consumer goods, given current
technology; spend on R&D to reduce unit emissions in the production
technology; increase capacity for abatement activity (in particular,
land use policies); augment family planning services and education
aimed at reducing the proportional growth rate of the population.
- 4.3
- The structure -- objective/ state variables/ control variables -- is
parallel to the optimization problem, but the goal is guidance and the
relations between state and control variables are semi-quantitative.
- 4.4
- For the moment we assume a constant population and a
constant unit emissions coefficient. This case gives three policy
instruments with which to guide the economy: two types of capital
investment (consumer goods production, abatement) plus the allocation
between current consumption and total investment. The latter refers
to the accounting identity by which national income is either spent on
current consumption or is saved and invested (increasing future
consumption capacity).
- 4.5
- The basic model is:
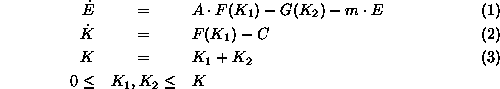
where 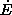 is the change per time period in the stock of emissions
E (ppm/time),
is the change per time period in the stock of emissions
E (ppm/time), 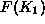 is the production function (GDP/time),
A is a
constant emissions coefficient (ppm/unit of GDP),
is the production function (GDP/time),
A is a
constant emissions coefficient (ppm/unit of GDP), 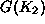 is
net emissions abated (ppm/time). In equation (1) we make
the assumption that all changes per time period in the
stock of emissions
is
net emissions abated (ppm/time). In equation (1) we make
the assumption that all changes per time period in the
stock of emissions 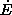 are due to anthropogenic
activity except for a natural proportional decay factor m. We have
implicitly assumed that all sinks for CO
are due to anthropogenic
activity except for a natural proportional decay factor m. We have
implicitly assumed that all sinks for CO 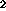 are full and we have not
considered fertilization feedback effects (for a full discussion see
(Wigley, 1993)). The production function
are full and we have not
considered fertilization feedback effects (for a full discussion see
(Wigley, 1993)). The production function 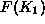 depends on capital
allocated to industrial production,
depends on capital
allocated to industrial production, 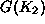 is a function of capital
allocated to the abatement sector. We assume that
is a function of capital
allocated to the abatement sector. We assume that 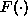 and
and 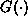 are monotonically increasing functions. The second equation derives
from the accounting identity of national income. Total investment
are monotonically increasing functions. The second equation derives
from the accounting identity of national income. Total investment
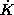 (GDP/time), that is, the change per time in total capital, is
what remains of national income after C (GDP/time) is
allocated to current consumption.
(GDP/time), that is, the change per time in total capital, is
what remains of national income after C (GDP/time) is
allocated to current consumption.
- 4.6
- The objective for the national authority is to invest in the various
activities in such a way as to ensure members of the economy a high
quality of life over time, by keeping consumption and environmental
index within acceptable ranges.
One way to understand how to achieve such an objective is to formulate
certain relationships between variables of the model and explore their
consequences.
The initial decision is the choice between consumption and total
investment (cfr. equation 2). We begin with a simple
assumption: that total investment is constant and positive, meaning
that the society is consuming less than it is producing

- 4.7
- The next decision is how to allocate investment (cfr. equation
3) between that used for consumers goods production (
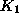 )
and that used for abatement (
)
and that used for abatement ( 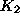 ). We choose a second simple rule:
invest an amount which is monotonically increasing with respect to the
total stock of emissions and numerically bounded by a pair of
increasing linear functions2
). We choose a second simple rule:
invest an amount which is monotonically increasing with respect to the
total stock of emissions and numerically bounded by a pair of
increasing linear functions2
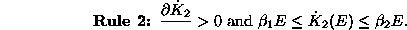
- 4.8
- Finally, a lower bound is established for investment in
production in order to keep up future consumption levels

- 4.9
- Acceptable trajectories are defined as those
for which per capita consumption does not decline below the original
value and emission levels do not reach boundary values. The
authority plans production so as to balance emissions with the
system's natural and anthropogenic capacity to abate emissions and
thereby guides the ecological system away from collapse and the
economic system away from low levels of per capita consumption. That
is, the authority's dynamic program for production must also be
sustainable.
 An Example
An Example
- 5.1
- In this section we illustrate how the problem discussed above can be
formulated and solved using SQPC.
The idea is to use SQPC's language to define a model of the domain
that can be reused to analyze different scenarios.
These scenarios will be explored to understand the effects of the
different rules mentioned above.
Domain Model
- 5.2
- Three steps need to be carried out in order to define a domain model.
First, the domain has to be conceptualized, that is entities and
relationships that will play some role in the definition of scenarios
have to be made explicit. The objective of such a step is to set a
basis upon which to define, case by case, the specific system being
analyzed as a set of interrelated instances of object types. By
declaring entities in the scenario, or by adding
or removing relationships between them, different scenarios can be
defined.
Second, types of quantities that are deemed useful need to be defined.
Instances of these types of quantities will be then automatically become
attributes of specific instances of objects and will be
included in models for the simulation.
Third, model fragments describing relevant and modular pieces of
equations among quantities of objects need to be defined.
- 5.3
- In our specific case, the taxonomy of the domain model consists of
objects and relationships like societies, that are embedded
within natural environments, that support a population
of individuals who are involved in socio-economic activities like
industrial production, pollution abatement and so forth.
Figure 2 shows some entities and relationships
included in the domain model.

Figure 2: Portion of the taxonomy of the domain model
- 5.4
- Several quantity types are then defined that characterize our
perspective on this domain, shown in fig. 3.

Figure 3: The definition of some quantity types
- 5.5
- At this point we can define model fragments. For example, a model
fragment might assert that for a society that supports a production
activity, and that evolves within an environment, then the amount of
emissions being released into the environment is positively influenced
by the amount of goods being produced and that emissions accumulate
over time to give the total amount of pollution present in the
environment.
- 5.6
- Figure 4 shows how these properties can be described.
Several other model fragments, not shown here, are encompassed by the
domain model that we use in this example.

Figure 4: A compositional model fragment
Scenario And Resulting Simulations
- 5.7
- The aim of the analysis is to evaluate the effects of previously
discussed rules of thumb and explore their variations.
The example centers on a situation in which there is a society (called
world) evolving in an environment (earth). The society
hosts a population (humans), it
supports an industrial production called (timber-prod) and one
kind of pollution abatement (smoke-filtering). A simple market exists
for timber that determines the price for this product.
- 5.8
- The situation is given to SQPC in terms of a scenario description
which includes these entities, their relationships, initial conditions
for some quantity, envelopes, and information about estimated changes
in some of the quantities. Figure 5 provides additional
details.

Figure 5: Part of the scenario definition
- 5.9
- The information specified in this scenario description is given to
SQPC that first decides which model fragments and envelopes
are applicable to this situation. Then it constructs a qualitative
model enriched with appropriate ranges and applicable envelopes.
Finally SQPC defines all the possible initial states that are
consistent with the conditions given in the scenario description and
simulates the model until the defined horizon is reached (in this case
a year).
- 5.10
- The objective of the authority is to keep the economic society on a
bounded path, but more specifically, it will try to avoid consumer
rebellion (per capita consumption declines) and environmental hell
(emissions hit an upper limit representing biosphere collapse). A
possible scenario could include Rules 1 and 2 only. No government
would adopt, however, such a set of rules: per capita consumption
would decline at some point for all trajectories. Our scenario
(figure 5) includes instead also Rule 3 and a
relatively small value for
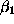 and
and 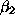 . Simulation of
this scenario up to the end of the time period of interest (i.e., after
one year) produces 9 behaviors (one of which is shown in figure
6). A common property of all such behaviors is that the
per capita consumption will necessarily increase (i.e., no rebellion
will take place). On the other hand, both a steady state in
environmental hell and increasing emissions beyond environmental hell
are plausible trajectories for the environmental index (like the behavior
shown in figure 6). To avoid this, the rational step is for the
decision-maker to increase investment in the abatement sector by
varying
. Simulation of
this scenario up to the end of the time period of interest (i.e., after
one year) produces 9 behaviors (one of which is shown in figure
6). A common property of all such behaviors is that the
per capita consumption will necessarily increase (i.e., no rebellion
will take place). On the other hand, both a steady state in
environmental hell and increasing emissions beyond environmental hell
are plausible trajectories for the environmental index (like the behavior
shown in figure 6). To avoid this, the rational step is for the
decision-maker to increase investment in the abatement sector by
varying 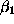 and
and 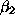 in Rule 2. Exploration of another
scenario, that is similar to the one presented above
(5) but that features a larger value of
in Rule 2. Exploration of another
scenario, that is similar to the one presented above
(5) but that features a larger value of 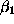 and
and
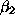 , shows that emissions decline in all the 4 predicted
behaviors, while maintaining an increasing per capita consumption.
Therefore, thanks to SQPC soundness, the policy-maker is guaranteed
that the last scenario, given the domain model, entails only
sustainable-solutions.
, shows that emissions decline in all the 4 predicted
behaviors, while maintaining an increasing per capita consumption.
Therefore, thanks to SQPC soundness, the policy-maker is guaranteed
that the last scenario, given the domain model, entails only
sustainable-solutions.
- 5.11
- Even in this very simple case, the advantages of using tools like SQPC
are that within a single domain model several different simulations
can be carried out quite easily, without requiring the user to define
complex executable models. Furthermore, even with very weak
quantitative information about functional relationships included in
the model certain kind of conclusions can be drawn. Finally, thanks to
the guaranteed coverage of the predicted solutions, the user of SQPC
knows that the predicted behaviors includes all the possible
trajectories of systems that are consistent with the given description.
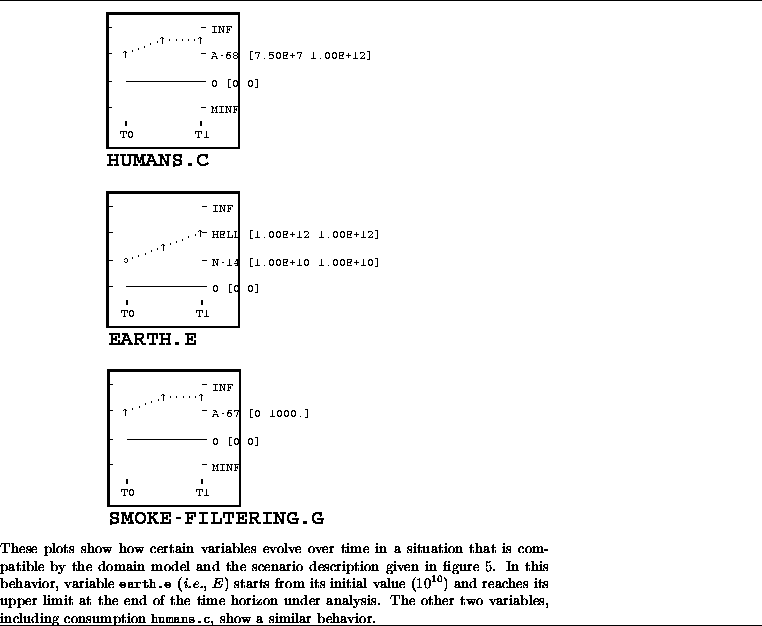
Figure 6: Plot of some variable for one of the predicted behaviors
 Related Work
Related Work
- 6.1
- Within the Artificial Intelligence field there are several
research directions that focus on socio-economic problems.
Farley and Lin (Farley and Lin, 1990, Lin and Farley, 1991) focus on qualitative models
of markets. They formulate economic theories (namely the law of demand
and supply) in terms of markets that give rise to stable dynamics.
That is, they see markets as homeostatic entities that support a
dynamic equilibrium. Markets are then used as building blocks for more
complex multi-market models, where interactions between markets are
represented and considered. For example, to explore how a
product market (representing income, investment and saving) may
interact with a money market (income and investment). Markets are
represented via purely qualitative relationships between variables.
Comparative statics methods are then used to determine the effects of
disequilibrium states on multiple interacting markets.
The simulation methods adopted are less general than the ones we
propose to use in this paper and in particular a simplifying
assumption is made that certain feedback loops are negligible, enabling a
stable trajectory to be followed.
The approach we presented in this paper is equation-based (in the
sense that there is no such thing as a predefined building-block like
the market) and therefore is more general. In addition, we provide
means for automatically assembling, on demand, an executable model
from a library of fragments of equations and for integrating in a
smooth way quantitative knowledge that may be available. Furthermore,
recently developed methods for specifying trajectory constraints (like
time-varying inputs or boundary condition problems)
(Brajnik and Clancy, 1996a, Brajnik and Clancy, 1998) can be easily
integrated into the architecture of SQPC, increasing in this way the
expressiveness of the approach and supporting a wider spectrum of
analyzes.
- 6.2
- In the framework of the global-warming problem, probabilistic
representations have been proposed. Distributions are given for
parameter values in (Hope et al., 1993, Dowlatabadi and Morgan, 1993) while a fuzzy decision
model is used in (Leimbach, 1996).
- 6.3
- The area of economic theory which has received most attention from the
AI perspective is the theory of choice, and in particular,
reasoning and rational choice, learning behavior, and adaptive
economic behavior (see e.g., Moss and Rae, 1992). Essentially this
approach assumes that the information set available, or obtainable, by
the decision-maker is so large that it is either impossible or
uneconomical to calculate the constrained optimization solution. This
issue is related to the existence of sufficient computational capacity
for resolving complex problems. If the economic agent is unable to
process the information it may resort to bounded rationality, or
procedural rationality. Moreover, if the decision maker is in a
disequilibrium situation, it may profit from experience, learn and
adapt. This characterization of economic agent as having limited
computational capacity but the ability to learn will be an interesting
field to watch as it comes to influence mainstream economic research.
- 6.4
- Another approach is that of artificial economies, wherein agents with
varying characteristics are allowed to act and be acted upon. This
provides a much more convincing economy than the usual one-agent or
n-similar agents assumption (for examples, see (Lane, 1993) and
(Bak et al., 1994)). An interesting project is currently being studied
by a group associated with the Santa Fe Institute who are building a
virtual stock market of around 100 agents who learn and adapt by
detecting patterns in price movements arising from their trading
(Stites, 1994).
- 6.5
- Expert systems have also been used in theoretical economics, see
(Artis et al., 1992) who argue that macro econometric models can be
improved by incorporating experts'
intuitive prediction rules into the models.
 Future Work And Conclusions
Future Work And Conclusions
- 7.1
- These preliminary results provide an indication of how a set of
rules of thumb can be validated by the decision maker using a
qualitative simulator, and an indication of the type of information
available for time paths of relevant variables. They show that even
with very poorly specified knowledge of models or scenarios certain
useful questions can be posed and answered.
- 7.2
- This should be a better base from which to make policy recommendations
for the systems with complicated trade-offs which are inherent to the
analysis of economic growth and environmental quality. Moreover,
these techniques make the maximum use of the qualitative information
that is available in economic theory. They also force the theorist to
formalize rules of thumb (i.e.,
specific policies/control laws) for
allocating between resources since optimization is no longer
available. We think that the use of such tools by students and
policy-makers could serve to deepen their understanding and intuitive
awareness of the complexity of dynamic allocation decision problems.
For the problem at hand, direct experience with game-like simulations
could greatly increase sensitivity to the delicate and controversial
questions which underlie the real world allocation problem.
- 7.3
- Future work will aim at introducing a further policy option for the
authority to deal with emissions -- investment in research and
development to reduce the technology coefficient (emissions per
output). We also intend to introduce demographic models of population
dynamics, which greatly complicates the time path for the per capita
consumption. Then yet another policy option will be available --
investment in a sector which provides health, family planning and
educational services, under the hypothesis that such investment
reduces the natural growth rate of the population.

 Acknowledgements
Acknowledgements
-
-
The simulations discussed and shown in the paper have been performed
using SQPC, a program developed by one of the authors. SQPC in turns
is based upon QSIM, a qualitative simulation system developed by the
Qualitative Reasoning Group at the Artificial Intelligence Laboratory,
The University of Texas at Austin led by prof. Ben Kuipers.
QSIM and other results of the Qualitative Reasoning Group are
accessible by World-Wide Web via
<http://www.cs.utexas.edu/users/qr>.
A special thanks goes to Bert Kay, who was tragically killed in Palo
Alto on June 12, 1997.

 Notes
Notes
- 1
- An extemal differential equation is automatically obtained from a
qualitative differential equation enriched with envelopes and gives
upper and lower bounds for each state variable. See
(Kay, 1996a) for details.
- 2
- The fact that bounding functions are linear should not lead to the
conclusion that the bounded functions should include only linear
functions.

 References
References
- Artis et al., 1992
-
M. Artis, S. Moss, and P. Ormerod.
The development of intelligent macroeconometric models and modelling
procedures.
In Moss and Rae, 1992, pages 167-176.
- Bak et al., 1994
-
P. Bak, K. Chen, J. Scheinkman, and M. Woodford.
Aggregate fluctuations from independent sectoral shocks:
self-organized criticality in a model of production and inventory dynamics.
Richerche Economiche, 47:3-30, 1994.
- Berleant and Kuipers, 1988
-
D. Berleant and B.J. Kuipers.
Using incomplete quantitative knowledge in qualitative reasoning.
In Proc. of the Sixth National Conference on Artificial
Intelligence, pages 324-329, 1988.
- Brajnik and Clancy, 1996a
-
G. Brajnik and D. J. Clancy.
Temporal constraints on trajectories in qualitative simulation.
In B. Clancey and D. Weld, editors, Proc. of the Tenth National
Conference on Artificial Intelligence, pages 979-984. AAAI Press, Aug.
1996.
- Brajnik and Clancy, 1996b
-
G. Brajnik and D. J. Clancy.
Temporal constraints on trajectories in qualitative simulation.
In Working papers of the Tenth International Workshop for
Qualitative Reasoning, pages 22-31, Fallen Leaf Lake, CA, May 1996.
AAAI Technical Report WS-96-01.
- Brajnik and Clancy, 1998
-
G. Brajnik and D. J. Clancy.
Focusing qualitative simulation using temporal logic: theoretical
foundations.
Annals of Mathematics and Artificial Intelligence, 1998.
To appear.
- Brajnik, 1995
-
G. Brajnik.
Introducing boundary conditions in semi-quantitative simulation.
In Ninth International Workshop on Qualitative Reasoning, pages
22-31, Amsterdam, May 1995.
- Dowlatabadi and Morgan, 1993
-
H. Dowlatabadi and M.G. Morgan.
A model framework for integrated studies of the climate problem.
Energy Policy, 21:209-221, 1993.
- Falkenhainer and Forbus, 1991
-
B. Falkenhainer and K. Forbus.
Compositional modeling: finding the right model for the job.
Artificial Intelligence, 51:95-143, 1991.
- Faltings and Struss, 1992
-
B. Faltings and P. Struss.
Recent advances in qualitative physics.
MIT Press, 1992.
- Farley and Lin, 1990
-
A. M. Farley and K. P. Lin.
Qualitative reasoning in economics.
Journal of Economic Dynamics and Control, 14:465-490, 1990.
North-Holland.
- Farquhar and Brajnik, 1994
-
A. Farquhar and G. Brajnik.
A semi-quantitative physics compiler.
In 8th International Workshop on Qualitative Reasoning about
physical systems, pages 81-89, Nara, Japan, 1994.
- Farquhar, 1994
-
A. Farquhar.
A qualitative physics compiler.
In Proc. of the 12th National Conference on Artificial
Intelligence, pages 1168-1174. AAAI Press / The MIT Press, 1994.
- Hope et al., 1993
-
C. Hope, J. Anderson, and P. Wenman.
Policy analysis of the greenhouse effect.
Energy Policy, 21:327-338, 1993.
- Iwasaki and Low, 1991
-
Y. Iwasaki and C. M. Low.
Model generation and simulation of device behavior with continuous
and discrete changes.
Technical Report KSL 91-69, Knowledge Systems Laboratory --
Stanford University, November 1991.
- Kay and Kuipers, 1993
-
H. Kay and B.J. Kuipers.
Numerical behavior envelopes for qualitative models.
In Proc. of the Eleventh National Conference on Artificial
Intelligence. AAAI Press/MIT Press, 1993.
- Kay, 1996a
-
H. Kay.
Refining Imprecise Models and Their Behaviors.
PhD thesis, Department of Computer Sciences, The University of Texas
at Austin, Dec 1996.
- Kay, 1996b
-
H. Kay.
SQsim: a simulator for imprecise ODE models.
TR AI96-247, University of Texas Artificial Intelligence Laboratory,
March 1996.
- Kay, 1997
-
H. Kay.
Robust identification using semiquantitative methods.
In IFAC Symposium on Fault Detection, Supervision and Safety for
Technical Processes (SAFEPROCESS'97), Hull, UK, Aug 1997.
- Kuipers, 1994
-
B.J. Kuipers.
Qualitative Reasoning: modeling and simulation with incomplete
knowledge.
MIT Press, Cambridge, Massachusetts, 1994.
- Lane, 1993
-
D. Lane.
Artificial worlds and economics, part II.
Journal of Evolutionaly Economics, 3:177-197, 1993.
- Leimbach, 1996
-
M. Leimbach.
Development of a fuzzy optimization model, supporting global warming
decision-making.
Environmental and Resource Economics, 7:163-192, 1996.
- Lin and Farley, 1991
-
K. P. Lin and A. M. Farley.
Qualitative economic reasoning: a disequilibrium perspective.
Computer Science in Economics and Management, 4:117-133, 1991.
- Moss and Rae, 1992
-
S. Moss and J. Rae.
Artificial Intelligence and Economic Analysis.
Edward Elgar, Hants, UK, 1992.
- Sebenius, 1984
-
J. K. Sebenius.
Negotiating the Law of the Sea.
Harvard University Press, Cambridge, 1984.
- Siebert, 1987
-
H. Siebert.
Economics of the Environment.
Springer-Verlag, Berlin, 1987.
- Stites, 1994
-
J. Stites.
W. Brian Arthur.
The Bulletin of the Santa Fe Institute, Winter:5-8, 1994.
- Wigley, 1993
-
T.M.L. Wigley.
Balancing the carbon budget. implications for projections of future
carbon dioxide concentration changes.
Tellus, 45(B):409-425, 1993.

 Return to Contents of this issue
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, 1998
![]() A version of this article in Portable Document Format (PDF) is also available. The PDF version is recommended if you want to print the article to a laser printer.
A version of this article in Portable Document Format (PDF) is also available. The PDF version is recommended if you want to print the article to a laser printer.![]()
 Abstract
Abstract![]()
![]() . Its meaning is given in terms of the subset of
continuous differentiable functions (
. Its meaning is given in terms of the subset of
continuous differentiable functions ( ![]() stands for the set of
real numbers extended with positive and negative infinity):
stands for the set of
real numbers extended with positive and negative infinity):
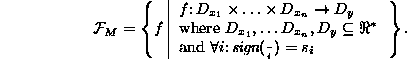
![]()

![]()
![]() means that in the
absence of countervailing influences, an increase in X
causes an increase in
Y. Furthermore, once we determine the set of influences
affecting Y,
Y is functionally determined by the influencing variables.
means that in the
absence of countervailing influences, an increase in X
causes an increase in
Y. Furthermore, once we determine the set of influences
affecting Y,
Y is functionally determined by the influencing variables.
![]() means that there exists a family of quantities
means that there exists a family of quantities
![]() , with
, with ![]() such that
such that ![]() . Similarly for
. Similarly for ![]() .
.
![]() ) expresses
the fact that if there are no other countervailing influences, a
positive value of X causes an increase of Y. Direct
influences are equivalent to algebraic influences on the derivative of the
influenced variable (i.e.,
) expresses
the fact that if there are no other countervailing influences, a
positive value of X causes an increase of Y. Direct
influences are equivalent to algebraic influences on the derivative of the
influenced variable (i.e.,
![]()
![]()
![]() ).
).
![]() is the change per time period in the stock of emissions
E (ppm/time),
is the change per time period in the stock of emissions
E (ppm/time), ![]() is the production function (GDP/time),
A is a
constant emissions coefficient (ppm/unit of GDP),
is the production function (GDP/time),
A is a
constant emissions coefficient (ppm/unit of GDP), ![]() is
net emissions abated (ppm/time). In equation (1) we make
the assumption that all changes per time period in the
stock of emissions
is
net emissions abated (ppm/time). In equation (1) we make
the assumption that all changes per time period in the
stock of emissions ![]() are due to anthropogenic
activity except for a natural proportional decay factor m. We have
implicitly assumed that all sinks for CO
are due to anthropogenic
activity except for a natural proportional decay factor m. We have
implicitly assumed that all sinks for CO ![]() are full and we have not
considered fertilization feedback effects (for a full discussion see
(Wigley, 1993)). The production function
are full and we have not
considered fertilization feedback effects (for a full discussion see
(Wigley, 1993)). The production function ![]() depends on capital
allocated to industrial production,
depends on capital
allocated to industrial production, ![]() is a function of capital
allocated to the abatement sector. We assume that
is a function of capital
allocated to the abatement sector. We assume that ![]() and
and ![]() are monotonically increasing functions. The second equation derives
from the accounting identity of national income. Total investment
are monotonically increasing functions. The second equation derives
from the accounting identity of national income. Total investment
![]() (GDP/time), that is, the change per time in total capital, is
what remains of national income after C (GDP/time) is
allocated to current consumption.
(GDP/time), that is, the change per time in total capital, is
what remains of national income after C (GDP/time) is
allocated to current consumption.
![]()
![]()
![]()





Return to Contents of this issue