| Number of possible states: | 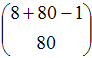 |
Joyce and colleagues (2006) published an interesting article where they propose an explanation for altruistic behaviour based on conditional association. To formalise and illustrate their ideas, they study a model where agents in a population subjected to evolutionary pressures are repeatedly paired to play a Prisoner's Dilemma game. Importantly, Joyce et al. (2006) abandon the common assumption of random encounters; this is a strong assumption that has been long known to play a crucial role in the emergence of cooperation (Eshel and Cavalli-Sforza 1982). Instead, agents in their model can break up partnerships depending on the previous action of their counterpart –a form of conditional association–. Besides this important point, the structure of Joyce et al.'s model is very similar to Axelrod's famous tournament and his “ecological analysis” (Axelrod 1984; Axelrod and Hamilton 1981).
The model comprises N agents. Each agent has a certain strategy out of a set S of 8 possible strategies. Each strategy determines the actions that the agent will take during the game (cooperate, defect or leave), conditioned to the previous action of his partner. For instance, an agent following strategy MOTH (acronym for “My way Or The Highway”) cooperates until his partner defects, in which case the agent following MOTH leaves. TIT FOR TAT (i.e. start by cooperating, repeat your partner's last action, and never leave) is also one of the 8 possible strategies. MOTH represents unconditional altruism which associates conditionally, whereas TIT FOR TAT represents conditional altruism which associates unconditionally.
Let us see the model in detail. A tournament consists of M matches which can be interpreted as different generations. Each match begins pairing the N agents at random to play a repeated Prisoner's Dilemma game. Agents play G iterations of the game in each match, and they do so potentially with the same partner, but not necessarily. The novelty of this tournament is the option given to the agents (i.e. to their strategies) to break up their current partnership unilaterally at any time during the match, and to associate with another agent –randomly chosen among the other unpaired agents– to continue playing the game. Once the match is finished, the S strategies are redistributed among the population proportionally to the total score obtained by the agents playing each strategy in the previous match [1]. Table 1 shows the payoff matrix considered in the model.
| Cooperate | Defect | |
| Cooperate | 3 , 3 | 0 , 5 |
| Defect | 5 , 0 | 1 , 1 |
| Table 1. Payoff matrix of the Prisoner's Dilemma game in Joyce et al.'s (2006) model. |
Joyce et al. (2006) explore the dynamics of their model in tournaments of 40 matches (M = 40) for different values of G (i.e. the number of iterations per match) and various initial conditions (i.e. the starting frequencies of each strategy). Here we analyse the first experiment presented in Joyce et al.'s paper using the concepts explained in our paper. Initially there are 10 agents for each of the possible strategies, i.e. 80 agents in total. We can represent the model as a THMC defining the state of the system as the number of agents following each possible strategy at the beginning of a match. Thus, the number of possible states is:
| Number of possible states: | 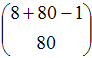 |
The THMC is observed at the beginning of each match (i.e. matches define the time-step of the THMC).
It is simple to verify that this THMC has several absorbing states. For example, all homogeneous states –where all the agents are following the same strategy– are absorbing states. Moreover, any combination of strategies ALL-C (always cooperate and never leave), TIT FOR TAT (start by cooperating, play as your partner did in the previous iteration and never leave), SANTA (cooperate once and leave) and MOTH (cooperate until your partner defects and then leave) is also an absorbing state of the THMC. All agents in any such combination obtain the same score in the match, since every agent in such a population always cooperates. Thus, the total score obtained by the set of agents following any of those 4 strategies is proportional to the number of agents following that strategy, and therefore the distribution of strategies in the new generation remains the same. Exactly the same happens with any combination of strategies ALL-D (always defect and never leave), HIT&RUN (defect once and leave), NASMOTH (defect until your partner defects and then leave) and NNHRUN (start by defecting and leave if your partner defects on the first iteration; otherwise, defect once more and leave). Any combination of these non-cooperative strategies is also an absorbing state. Analogously to the previous case, all agents in any such combination obtain the same score in the match, since every agent in such a population always defects.
More generally, a state is absorbing if and only if any possible pairing of the agents in the state leads to the same average payoff (across agents) for every strategy.
It is important to notice that our conclusions derive from the specific selection mechanism implemented in Joyce et al.'s (2006) model, which does not allow for genetic drift. For instance, if the authors had implemented a roulette wheel selection mechanism, the heterogeneous absorbing states described above would not be absorbing anymore. Similarly, if mutation could occur in any state, then not even the homogeneous states would be absorbing. Furthermore, if the mutation mechanism is such that any agent may randomly change its strategy in between matches, then the THMC becomes irreducible and aperiodic (see sufficient condition (i) in Proposition 4), so initial conditions would be immaterial in the long run.
The differences between the dynamics of this model and the dynamics of other evolutionary models analysed in this appendix (e.g. Axelrod's metanorms models and Takahashi's models of generalized exchange) stem from the fact that Joyce et al.'s (2006) model lacks any diversity-generating mechanism. There is no strategy recombination and no mutation, noise or error; thus, strategies that are not present in the population at any given time cannot appear at any subsequent time. In other words, if there are strategies in state j that are not present in state i, then j is not accessible from i.
AXELROD R M (1984) The Evolution of Cooperation. New York: Basic Books.
AXELROD R M and Hamilton W D (1981) The Evolution of Cooperation. Science, 211(4489), pp. 1390-1396
ESHEL, I. and L. L. Cavalli-Sforza (1982). Assortment of Encounters and Evolution of Cooperativeness. Proceedings of the National Academy of Sciences of the United States of America 79(4), pp. 1331-1335.
JOYCE D, Kennison J, Densmore O, Guerin S, Barr S, Charles E, and Thompson N S (2006) My Way or the Highway: a More Naturalistic Model of Altruism Tested in an Iterative Prisoners' Dilemma. Journal of Artificial Societies and Social Simulation, 9(2)4. https://www.jasss.org/9/2/4.html.
1 This process can be understood as the selection mechanism of the model dynamics.