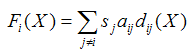
Axelrod and Bennett (1993) propose a model to analyse the formation of coalitions in different domains. The model has been successfully used to reproduce the alignment of European countries in the Second World War (Axelrod and Bennett 1993) and, with some refinements, to analyse the coalition formation of standard-setting alliances in UNIX operating systems (Axelrod et al. 1995). Axelrod and Bennett's model has been redefined and formally analysed by Galam (1996).
In Axelrod and Bennett's model each actor i is a member of one of two competing coalitions. Actor i decides to leave her current coalition or stay in it by comparing her current frustration with the frustration she would have if she joined the opposite coalition. Actor i's frustration depends on her affinity aij with each of the other actors j ≠ i and on the value of some intrinsic property of each actor j denoted by sj (representing e.g. j's size or influence). To be precise, actor i's frustration with a certain configuration X (i.e. a certain partition of the actors into two coalitions) is denoted by Fi(X) and calculated as follows:
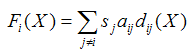
where dij(X) measures the distance between actors i and j in configuration X: dij(X) = 0 if actors i and j belong to the same coalition in configuration X, and dij(X) = 1 if they are in different coalitions. Affinities between actors are symmetric (i.e. aij = aji). To study the dynamics of the system, Axelrod and Bennett (1993) make the incremental assumption: only one single actor can switch coalition at a time, and this movement must imply a reduction in the actor's frustration. To identify the most stable configurations there is no need to define the details about how actors are selected to consider a possible move as long as we assume that no actor who wants to change coalition is permanently prevented from doing so.
To analyse this model within the Markov chain framework let us define the state of the system as a certain configuration. The number of possible states is the number of possible configurations, i.e. 2n/2, where n is the number of actors and the dividend 2 accounts for the symmetry in the system (any actor can be in one of the sides, but which side is considered first is arbitrary).
The incremental assumption guarantees that any state where no actor wants to change coalition unilaterally is absorbing. The assumption "no actor who wants to change coalition is permanently prevented from doing so" guarantees that any state where there is at least one actor who wants to change coalition is not absorbing. Thus, a state is absorbing if and only if no actor wants to change coalition unilaterally. In game theory terms, a state is absorbing if and only if it is a Nash equilibrium.
Since it is possible to reach (at least) one absorbing state from any given state [1], we can assert that there isn't any closed communicating class with more than one state in the model. Therefore, following Proposition 2 we can partition the state space as: S = {abs1} ∪ {abs2} ∪ … ∪ {absk} ∪ T, where abs1, abs2, … , absk are absorbing states, and T is the union of all non-closed communicating classes. Taking into account Proposition 3 we can conclude that sooner or later the THMC will enter one of the absorbing states and stay in it forever.
Axelrod and Bennett (1993) define a concept which is particularly useful to identify absorbing states: the total energy of the system in configuration X. The total energy is denoted by E(X) and calculated as follows:
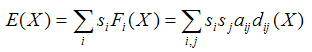
This definition is convenient because, given that affinities are symmetric, it is not difficult to prove that any movement under the incremental assumption implies a reduction in the total energy of the system (Axelrod and Bennett 1993; Axelrod et al. 1995), and absorbing states correspond to states where the energy has reached a local minimum [2]. In this way, Axelrod and Bennett's (1993) formula nicely captures the idea –inherited from physics– that systems tend to move towards states of low energy.
In their study of the European coalitions in WWII, Axelrod and Bennett (1993) do not analyse the dynamics of the model; instead they calculate the total energy of the system for every possible configuration of the 17 considered countries. With their parameters, the system has only two local minima (i.e. two absorbing states) and one of them brilliantly approximates the Allies and the Axis coalitions in the conflict.
If we actually implemented and ran a simulation model satisfying the assumptions made here, we would see that the system would necessarily end up in one of these two absorbing states. The probability of finishing in one configuration or the other would depend on the initial conditions.
AXELROD R M and Bennett D S (1993) A Landscape Theory of Aggregation. British Journal of Political Science, 23(2), pp. 211-233
AXELROD R M, Mitchell W, Thomas R E, Bennett D S, and Bruderer E (1995) Coalition Formation in Standard-Setting Alliances. Management Science, 41(9), pp. 1493-1508
GALAM S (1996) Fragmentation versus stability in bimodal coalitions. Physica A: Statistical Mechanics and its Applications, 230(1-2), pp. 174-188
1 The validity of this statement can be easily appreciated using the definition of the total energy of the system derived by Axelrod and Bennett (1993).
2 A configuration is a local minimum if and only if there is no unilateral change of coalition that reduces the energy of the system.